Магазин
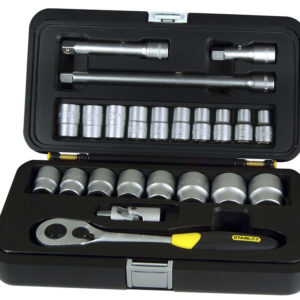
Вас приветствует интернет-магазин, в котором вы сможете приобрести ручной и профессиональный инструмент, шиномонтажное оборудование, автомобильные компрессоры. Нашей задачей является сделать вашу жизнь комфортнее и удобнее, так как именно у нас вы сможете подобрать нужный товар за весьма короткое время и по довольно низкой цене, а также узнать его применение перейдя по ссылке https://goncharyk.com.ua/. Таким образом, наши клиенты могут приобрести нужную им технику и информацию, не выходя из дома и практически не утруждая себя.
Советуем также нашим посетительницам посетить женский блог https://kite.od.ua/, из которого вы сможете взять много полезных советов.
Отображение 1–12 из 60 результатов